ملاحظات و احتیاطات در کاربست مدل‌های ریاضی انتشار بیماری برای سیاست‌گذاری

هنگام شیوع یک بیماری واگیردار نوظهور، سیاست‌گذار نیاز به شناخت پارامترهای کلیدی دخیل در شیوع بیماری (مانند نرخ مرگ‌ومیر) و برآورد اثر مداخله‌های مختلف غیردارویی (مثل تعطیلی مدارس) بر متغیرهای مختلف تصمیم‌گیری دارد. اهم متغیرهای تصمیم‌گیری برای سیاست‌گذار عبارتند از تعداد ابتلا و مرگ‌ومیر در سناریوهای مختلف، بیشینه‌ی تعداد مبتلایان و زمان رخ‌داد آن، تعداد تخت بیمارستانی، اتاق آی‌سی‌یو و دستگاه تنفس مورد نیاز، و پیش‌بینی سیر انتشار بیماری (شکل ۱). اما اکوسیستم شیوع چنین بیماری‌هایی، یک سیستم پیچیده است. به این معنا که نه تنها تعداد عوامل اثرگذار بر رفتار سیستم و ارتباطات بین آن‌ها زیاد است، بلکه تعامل این عوامل با یکدیگر نیز ممکن است منجر به ظهور رفتارهای غیرقابل‌ پیش‌بینی شود. به عنوان مثال تقارن اعمال فاصله‌گیری اجتماعی با آغاز فصل بهار ممکن است منجر به بروز نافرمانی هماهنگ طبقاتی از جامعه از فرامین حاکمیت شود. پیش‌بینی رفتار چنین سیستم‌هایی در سناریوهای مختلف بسیار دشوار و نیازمند استفاده از داده‌ها و مدل‌های پیشرفته است.

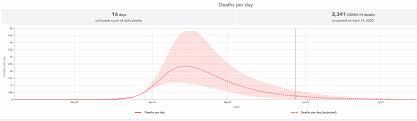
شکل ۱: برآورد تعداد مرگ‌ومیر ناشی از کرونا در شهر نیویورک توسط مدل شبیه‌سازی دانشگاه واشینگتن[۱]

[۱] http://www.healthdata.org/research-article/forecasting-covid-19-impact-hospital-bed-days-icu-days-ventilator-days-and-deaths

مدل‌های کلاسیک اپیدمی‌ها از دهه ۱۹۲۰ و با استفاده از معادلات دیفرانسیل آغاز شدند. این مدل‌ها فرض می‌کردند که جمعیت کاملا همگن است و افراد سیر «مستعد دریافت ویروس»، «مبتلا شدن»، و «بهبود/مرگ» را طی می‌کنند. مهم‌ترین دستاورد این مدل‌ها ارائه فرضیه‌ی «ایمنی گله‌ای» بود، که در آن ایمن شدن بخشی از جامعه باعث فرونشاندن شیوع و محافظت از کل جامعه می‌شود. اما این مدل‌ها برای درنظرگرفتن ساختار پیچیده و غیرهمگن روابط اجتماعی و تعاملات مستقیم افراد، که ممکن است رفتار خود را بر اساس میزان شیوع بیماری تنظیم کنند (شاید حتی غیرمنطقی)، مناسب نبود[۱]. با ظهور بیماری ایدز در اواخر دهه ۸۰ و افزایش اهمیت شبکه روابط مستقیم افراد در شیوع آن، تلاش‌ها برای معرفی مدل‌‌های ریاضی مناسب‌تر برای شبیه‌سازی انتشار بیماری‌های واگیردار که دربرگیرنده‌ی جزئیات فردی و اجتماعی باشد (مانند مدل‌های عامل/فردـ‌محور) وارد مرحله جدیدی شد و در ادامه برای مدل‌سازی انتشار سایر بیماری‌ها مانند سرخک، آبله، آنفولانزا، و اِبولا استفاده شد (به عنوان نمونه رجوع شود به Epstein and Axtell 1996[۲]).

در روزها و هفته‌های اخیر نیز شاهد اخبار مختلفی از پیش‌بینی کیفی یا کمّی این مدل‌ها از سیر انتشار کرونا در ایران و سایر کشورها بوده‌ایم که پیش‌بینی‌های بعضا بسیار متفاوتی از متغیرهای تصمیم ارائه داده‌اند، اما در برخی موارد منجر به تغییر سیاست‌گذاری کشورها شده‌اند. معروف‌ترین نمونه آن، مدل فرد‌ـ‌محور کووید۱۹ دانشگاه امپریال کالج انگلستان است که با پیش‌بینی تعداد بالای مرگ‌ومیر در صورت عدم اعمال مداخله‌ها سخت‌گیرانه، باعث تغییر سیاست دولت انگلستان، تاثیر بر سیاست‌های دولت آمریکا، و هشدار برای فرانسه شد[۳].

اما نتایج این مدل‌ها (به‌خصوص نتایج کمّی) تا چه حد قابل اعتماد است، علت وجود تفاوت‌ فاحش بین آن‌ها چیست، و آیا انتشار رسانه‌ای آن‌ها اقدام موثری است؟ اگرچه شبیه‌سازی مبتنی بر مدل‌های ریاضی بهترین ابزار موجود برای مدل‌سازی چنین سیستم‌های پیچیده‌ نوظهور است و چارچوبی کلی برای شناخت کلان سیستم و بررسی اثر مداخله‌های مختلف برای سیاست‌گذار را فراهم می‌کند[۴]، قصد داریم در این نوشتار با بیان دشواری و محدودیت‌های موجود برای توسعه این مد‌ل‌ها علت غیرقابل‌ اتکا بودن نتایج عددی اکثر آن‌ها برای سیاست‌گذاران را شرح دهیم و نیز بحثی در خصوص مضرات احتمالی انتشار عمومی آن‌ها بر افکار عمومی داشته باشیم.

در ادامه، ابتدا پنج دسته کلی از محدودیت‌های این‌ مدل‌ها (خصوصا در کشورهای درحال توسعه) را توصیف می‌کنیم. سپس با بیان اهداف مختلف متصور از ارائه مدل‌های ریاضی شیوع بیماری و در نظرگرفتن محدودیت‌های بحث‌شده، چارچوبی کلی برای ارائه نتایج این مدل‌ها پیشنهاد می‌کنیم. در انتها نیز با اشاره مختصر به سوگیری‌های شناختی موجود در انسان، پژوهش‌گران محترم را دعوت به رسانه‌ای نکردن نتایج عددی خود در صورت عدم توسعه مدل قوی و حاوی جزئیات کافی می‌نمائیم.

[۱] Epstein, J. M. (2009). Modelling to contain pandemics. Nature, ۴۶۰(۷۲۵۶), ۶۸۷-۶۸۷٫

[۲] Epstein, J. M., & Axtell, R. (1996). Growing artificial societies: social science from the bottom up. Brookings Institution Press.

[۳] https://www.washingtonpost.com/world/europe/a-chilling-scientific-paper-helped-upend-us-and-uk-coronavirus-strategies/2020/03/17/aaa84116-6851-11ea-b199-3a9799c54512_story.html

[۴] Dobson, A. (2014). Mathematical models for emerging disease. Science, ۳۴۶(۶۲۱۵), ۱۲۹۴-۱۲۹۵٫

متن کامل این گزارش از طریق لینک زیر قابل‌دسترسی است:

دانلود فایل